For Which Positive Integers K Is the Following Series Convergent

N are irrational. If the initial term of an arithmetic progression is and the common difference of successive members is then the -th.

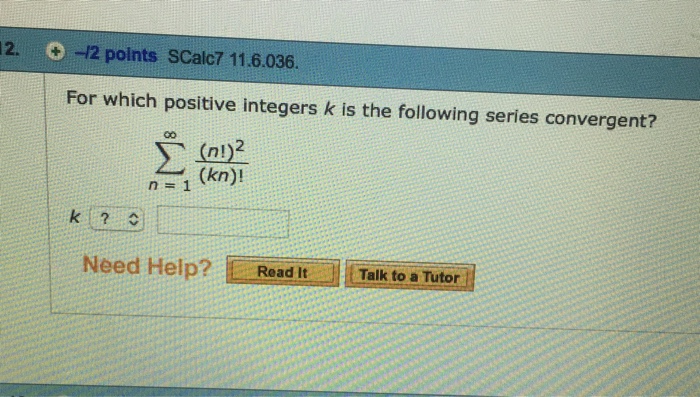
Solved For Which Positive Integers K Is The Following Series Chegg Com

F n a n f n a n for all integers n 1.

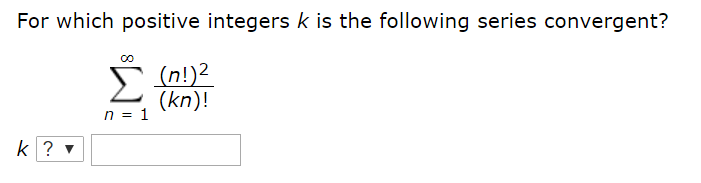
. There are also results on the irrationality of values of the Riemann zeta function at the elements of certain subsets of the positive odd integers. F f is continuous f f is decreasing and. An arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant.

Suppose there exists a function f f satisfying the following three conditions. N 1 a n. Suppose n 1 a n n 1 a n is a convergent series with positive terms.

It is known that ζ3 is irrational Apérys theorem and that infinitely many of the numbers ζ2n 1. Let S N S N be the Nth partial sum of n 1 a n. For example at least one of ζ5 ζ7 ζ9 or ζ11 is irrational.

Is an arithmetic progression with a common difference of 2. For instance the sequence 5 7 9 11 13 15.

For Which Positive Integers Of K Is Series Convergent N Kn Youtube

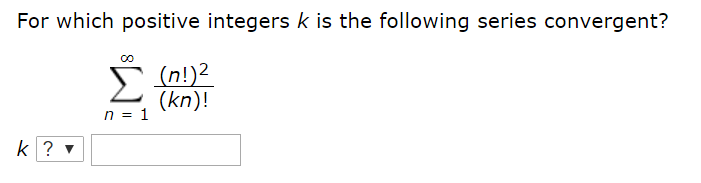
Solved For Which Positive Integers K Is The Following Series Chegg Com

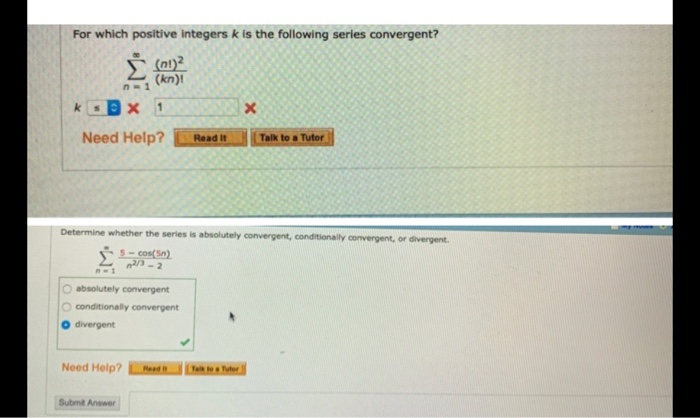
Solved For Which Positive Integers K Is The Following Series Chegg Com